# Lasso
```{r setup, echo=FALSE}
knitr::opts_chunk$set(fig.path="Ch11-figures/")
```
This goal of this chapter is to create an interactive data
visualization that explains the
[Lasso](https://en.wikipedia.org/wiki/Lasso_%28statistics%29), a
machine learning model for regularized linear regression.
Chapter outline:
* We begin with several static data visualizations of the lasso path.
* We then create an interactive version with a facet and plot showing
subtrain/validation error and residuals.
* Finally we re-design the interactive data visualization with
simplified legends and moving tallrects.
## Static plots of the coefficient regularization path {#static-path-plots}
We begin by loading the prostate cancer data set.
```{r}
if(!requireNamespace("animint2data"))
remotes::install_github("animint/animint2data")
data(prostate, package="animint2data")
library(data.table)
print(prostate, topn=1, trunc.cols = TRUE)
```
The output above shows the first and last row of the data table.
The `train` column indicates a pre-defined split in the data.
In this visualization, we will study the regularization path of the Lasso, for which we need a hold-out set to learn the optimal degree of regularization.
We will use the split set name `subtrain` for the data used to compute linear model coefficients, and `validation` for the data used for selecting the regularization parameter (by minimizing prediction error on this set).
```{r}
prostate[
, set := ifelse(train, "subtrain", "validation")
][, table(set)]
```
We construct subtrain inputs `x` and outputs `y` using the code below.
```{r}
input.cols <- c(
"lcavol", "lweight", "age", "lbph",
"svi", "lcp", "gleason", "pgg45")
prostate.inputs <- prostate[, ..input.cols]
is.subtrain <- prostate$set == "subtrain"
x <- as.matrix(prostate.inputs[is.subtrain])
head(x)
y <- prostate[is.subtrain, lpsa]
head(y)
```
Below we fit the full path of lasso solutions using the `lars` package.
```{r}
library(lars)
fit <- lars(x,y,type="lasso")
fit$lambda
```
The path of `lambda` values are not evenly spaced.
```{r}
pred.nox <- predict(fit, type="coef")
beta <- scale(pred.nox$coefficients, FALSE, 1/fit$normx)
arclength <- rowSums(abs(beta))
path.list <- list()
for(variable in colnames(beta)){
standardized.coef <- beta[, variable]
path.list[[variable]] <- data.table::data.table(
step=seq_along(standardized.coef),
lambda=c(fit$lambda, 0),
variable,
standardized.coef,
fraction=pred.nox$fraction,
arclength)
}
path <- do.call(rbind, path.list)
variable.colors <- c(
"#E41A1C", "#377EB8", "#4DAF4A", "#984EA3", "#FF7F00", "#FFFF33",
"#A65628", "#F781BF", "#999999")
library(animint2)
gg.lambda <- ggplot()+
theme_bw()+
theme(panel.margin=grid::unit(0, "lines"))+
scale_color_manual(values=variable.colors)+
geom_line(aes(
lambda, standardized.coef, color=variable, group=variable),
data=path)
gg.lambda
```
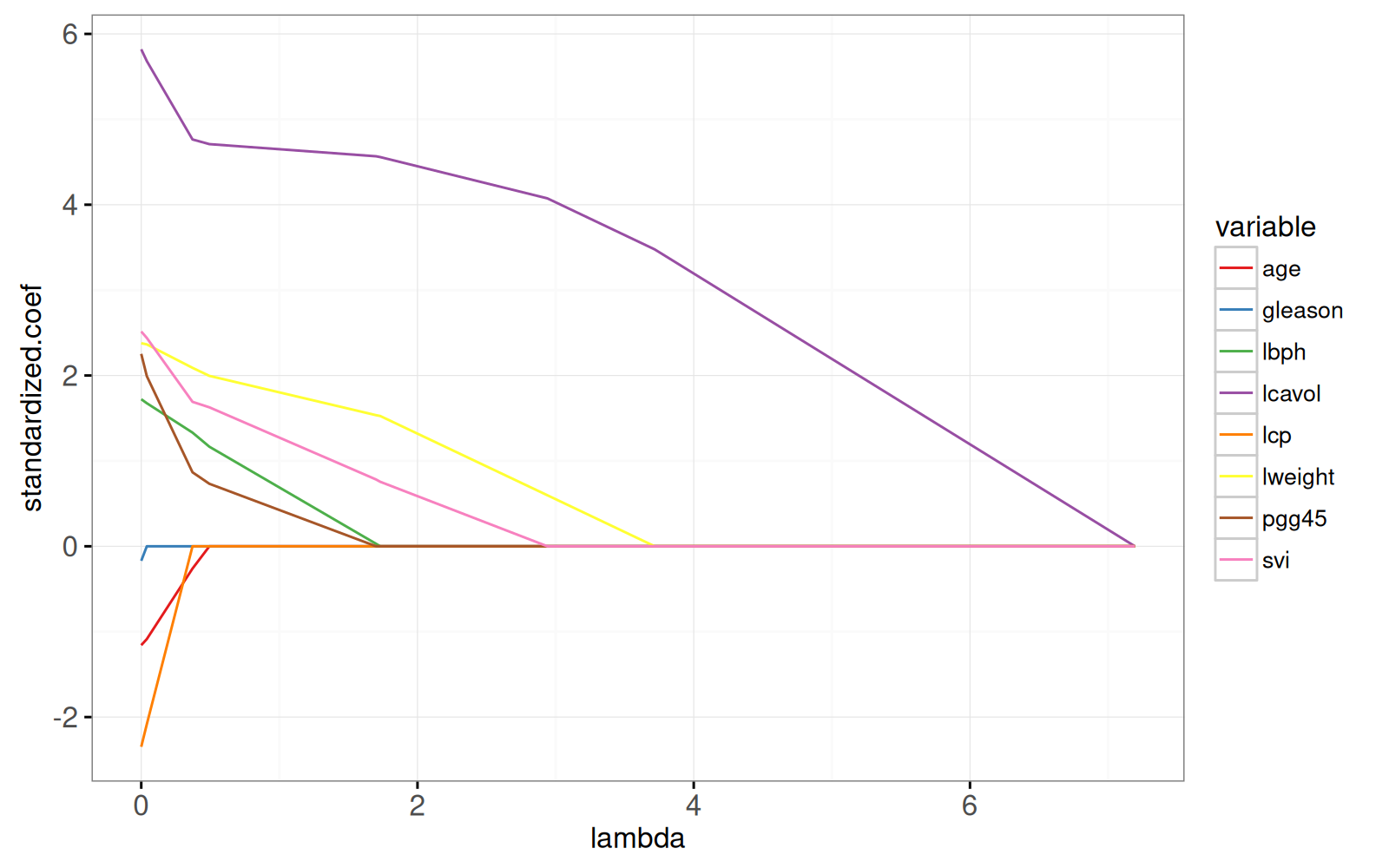
The plot above shows the entire lasso path, the optimal weights in the
L1-regularized least squares regression problem, for every
regularization parameter lambda. The path begins at the least squares
solution, lambda=0 on the left. It ends at the completely regularized
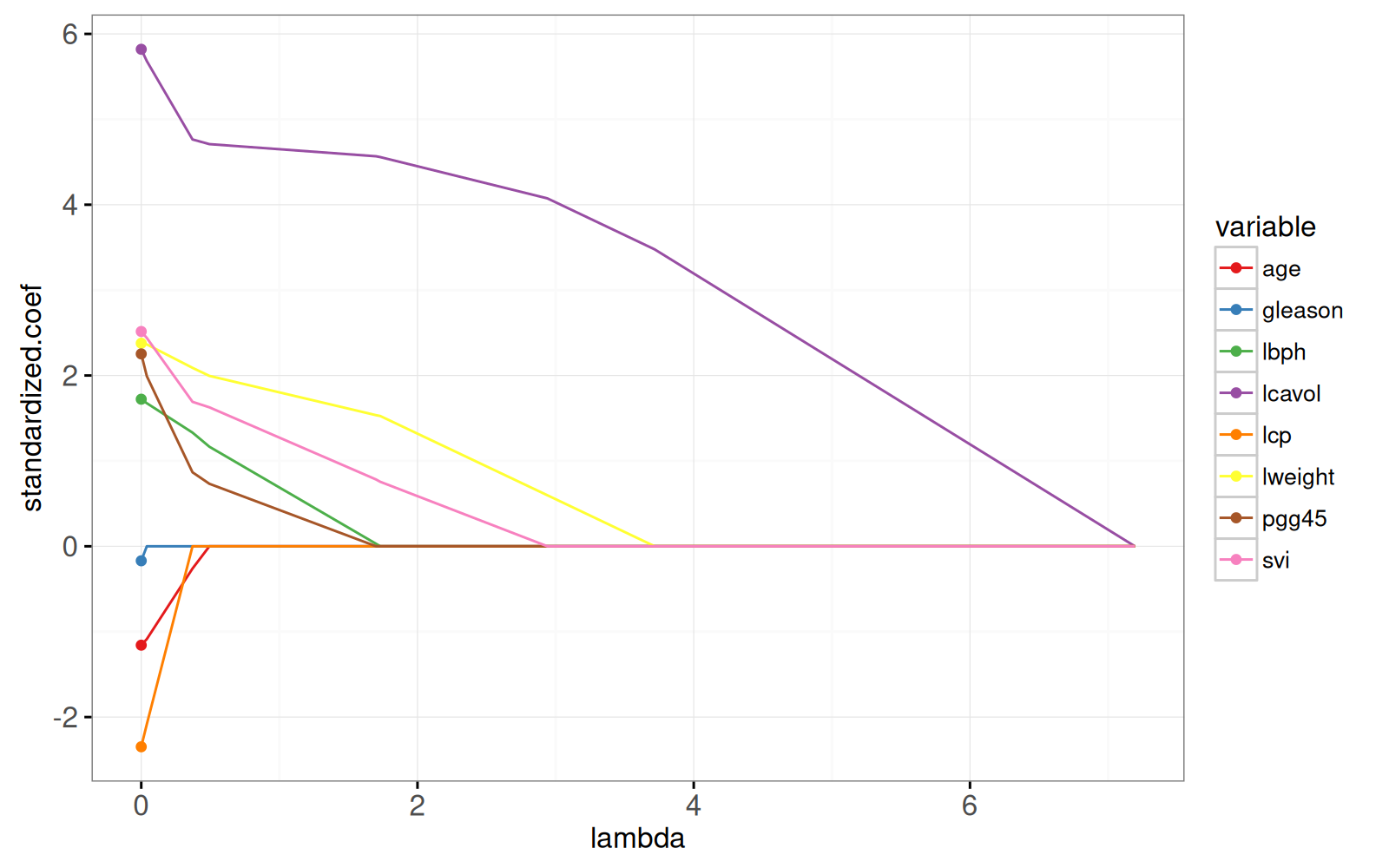
intercept-only model on the right. To see the equivalence with the
ordinary least squares solution, we add dots in the plot below.
```{r}
x.scaled <- with(fit, scale(x, meanx, normx))
lfit <- lm.fit(x.scaled, y)
lpoints <- data.table::data.table(
variable=colnames(x),
standardized.coef=lfit$coefficients,
arclength=sum(abs(lfit$coefficients)))
gg.lambda+
geom_point(aes(
0, standardized.coef, color=variable),
data=lpoints)
```
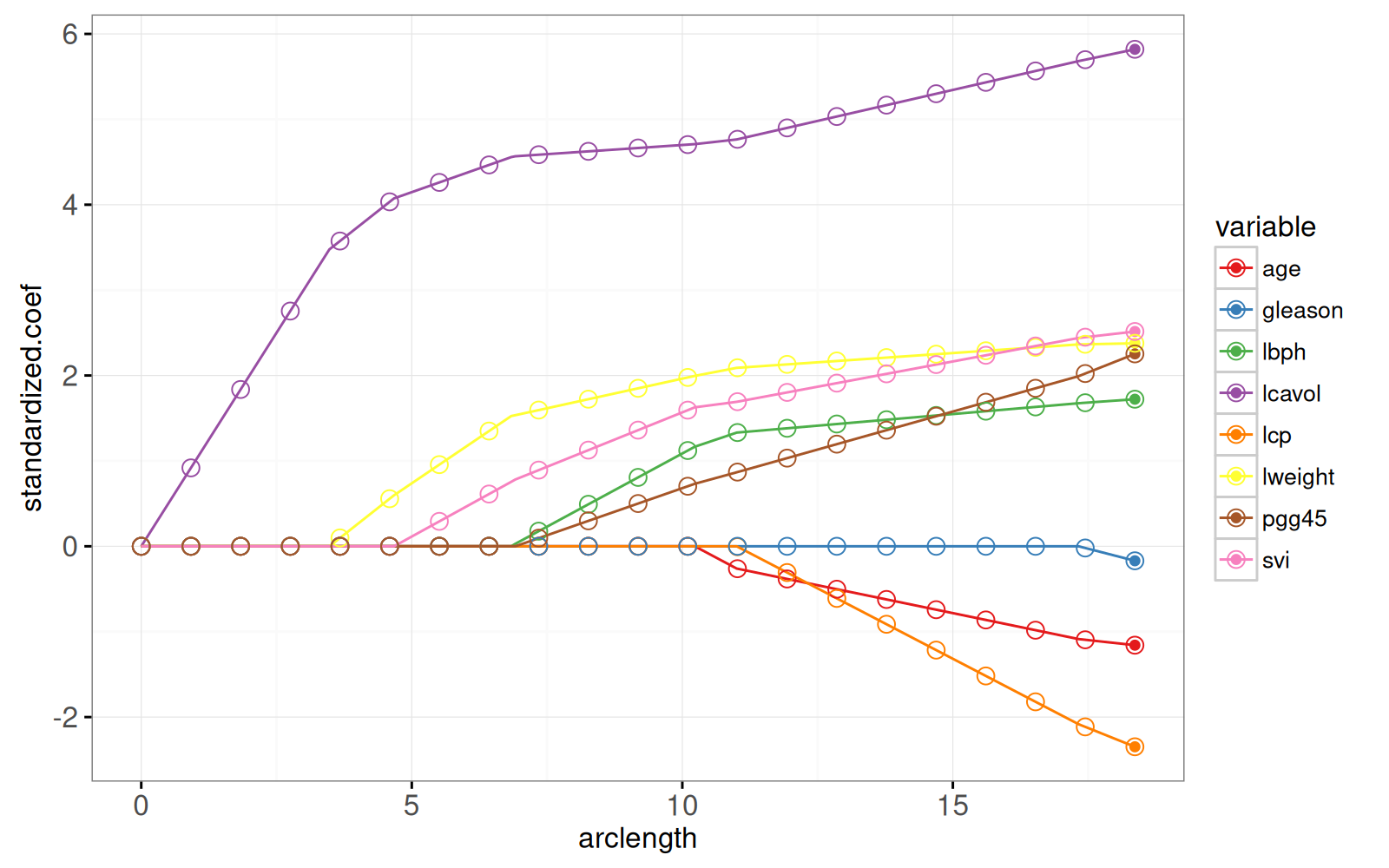
In the next plot below, we show the path as a function of L1 norm
(arclength), with some more points on an evenly spaced grid that we
will use later for animation.
```{r}
fraction <- sort(unique(c(
seq(0, 1, l=21))))
pred.fraction <- predict(
fit, prostate.inputs,
type="coef", mode="fraction", s=fraction)
coef.grid.list <- list()
coef.grid.mat <- scale(pred.fraction$coefficients, FALSE, 1/fit$normx)
for(fraction.i in seq_along(fraction)){
standardized.coef <- coef.grid.mat[fraction.i,]
coef.grid.list[[fraction.i]] <- data.table::data.table(
fraction=fraction[[fraction.i]],
variable=colnames(x),
standardized.coef,
arclength=sum(abs(standardized.coef)))
}
coef.grid <- do.call(rbind, coef.grid.list)
ggplot()+
theme_bw()+
theme(panel.margin=grid::unit(0, "lines"))+
scale_color_manual(values=variable.colors)+
geom_line(aes(
arclength, standardized.coef, color=variable, group=variable),
data=path)+
geom_point(aes(
arclength, standardized.coef, color=variable),
data=lpoints)+
geom_point(aes(
arclength, standardized.coef, color=variable),
shape=21,
fill=NA,
size=3,
data=coef.grid)
```
The plot above shows that the weights at the grid points are
consistent with the lines that represent the entire path of
solutions. The LARS algorithm quickly provides Lasso solutions for as
many grid points as you like. More precisely, since the LARS only
computes the change-points in the piecewise linear path, its time
complexity only depends on the number of change-points (not the number
of grid points).
## Interactive visualization of the regularization path {#interactive-path-viz}
In this section, we combine the lasso weight path with the subtrain/validation error plot.
First, we compute a data table with one row per model size and set.
```{r}
pred.list <- predict(
fit, prostate.inputs,
mode="fraction", s=fraction)
residual.mat <- pred.list$fit - prostate$lpsa
squares.mat <- residual.mat * residual.mat
mean.error <- prostate[, data.table(
fraction,
mse=colMeans(squares.mat[.I, ]),
arclength=rowSums(abs(coef.grid.mat))
), by=set]
print(mean.error, topn=2)
```
Note in the code above that we used the data table special symbol `.I`, which is set to the indices corresponding to the current value of `by=set`, used to compute the `mse` for each set.
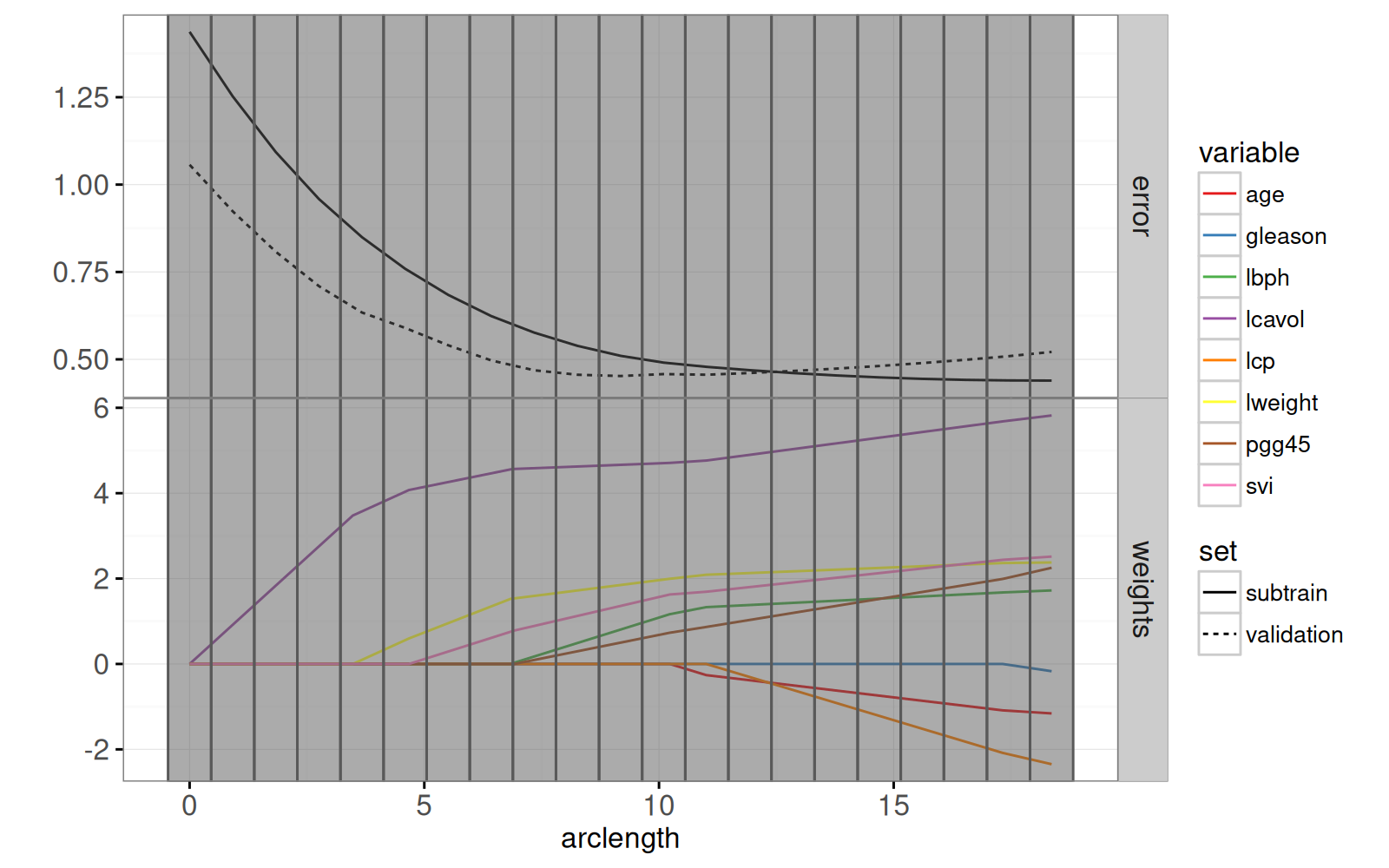
The table in the output above is used to plot the error curves below.
```{r}
rect.width <- diff(mean.error$arclength[1:2])/2
addY <- function(dt, y){
data.table::data.table(dt, y.var=factor(y, c("error", "weights")))
}
tallrect.dt <- coef.grid[variable==variable[1],]
gg.path <- ggplot()+
theme_bw()+
theme(panel.margin=grid::unit(0, "lines"))+
theme_animint(width=300, rowspan=1)+
facet_grid(y.var ~ ., scales="free")+
ylab("")+
scale_color_manual(values=variable.colors)+
geom_line(aes(
arclength, standardized.coef, color=variable, group=variable),
data=addY(path, "weights"))+
geom_line(aes(
arclength, mse, linetype=set, group=set),
data=addY(mean.error, "error"))+
geom_tallrect(aes(
xmin=arclength-rect.width,
xmax=arclength+rect.width),
clickSelects="arclength",
alpha=0.5,
data=tallrect.dt)
gg.path
```
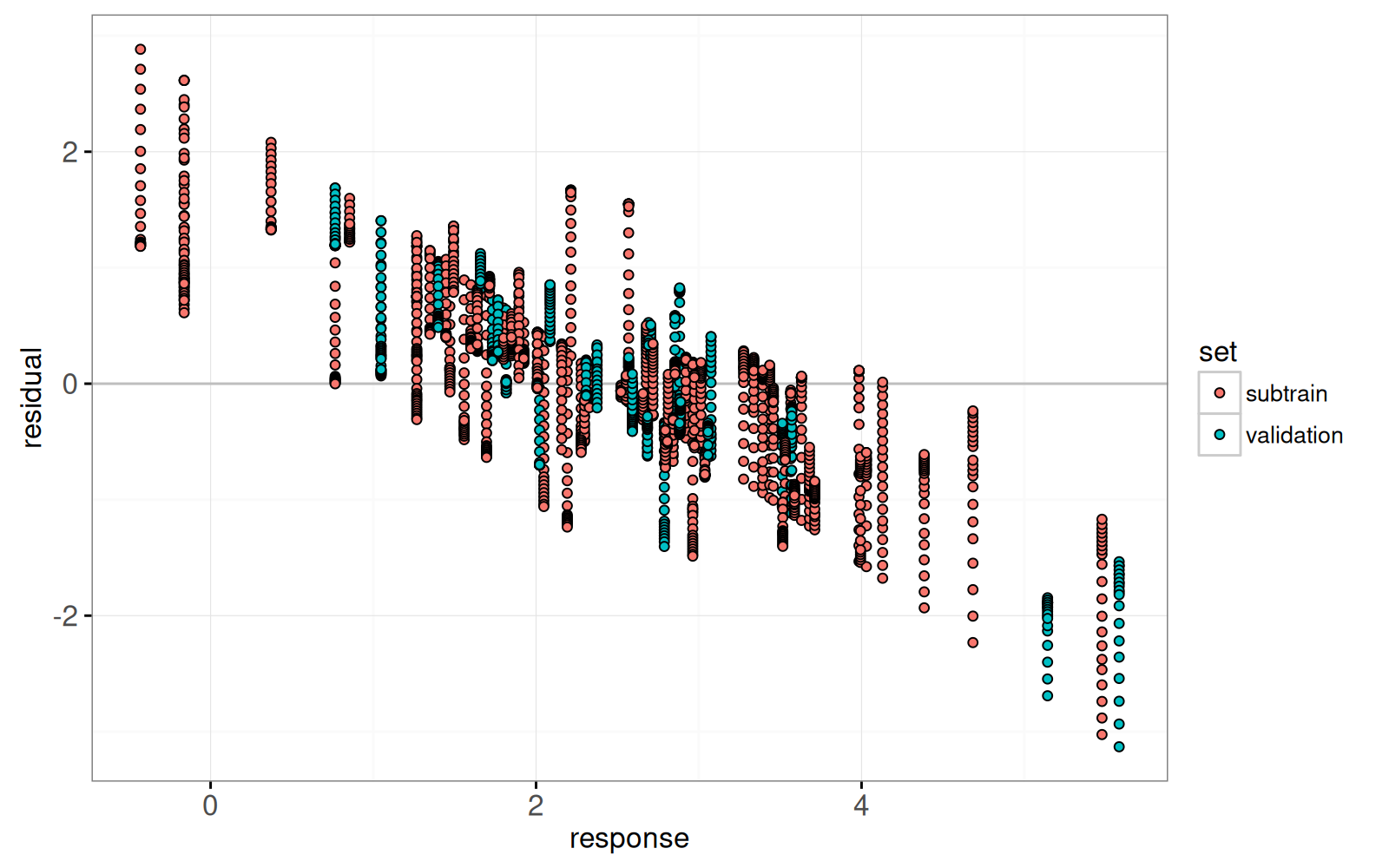
Finally, we add a plot of residuals versus actual values.
```{r}
lasso.res.list <- list()
for(fraction.i in seq_along(fraction)){
lasso.res.list[[fraction.i]] <- data.table::data.table(
observation.i=1:nrow(prostate),
fraction=fraction[[fraction.i]],
residual=residual.mat[, fraction.i],
response=prostate$lpsa,
arclength=sum(abs(coef.grid.mat[fraction.i,])),
set=prostate$set)
}
lasso.res <- do.call(rbind, lasso.res.list)
hline.dt <- data.table::data.table(residual=0)
gg.res <- ggplot()+
theme_bw()+
geom_hline(aes(
yintercept=residual),
data=hline.dt,
color="grey")+
geom_point(aes(
response, residual, fill=set,
key=observation.i),
showSelected="arclength",
shape=21,
data=lasso.res)
gg.res
```
Below, we combine the ggplots above in a single animint
below. Clicking the first plot changes the regularization parameter,
and the residuals that are shown in the second plot.
```{r Ch11-viz-one-split}
animint(
gg.path,
gg.res,
duration=list(arclength=2000),
time=list(variable="arclength", ms=2000))
```
## Re-design with moving tallrects {#re-design}
The re-design below has two changes. First, you may have noticed that
there are two different set legends in the previous animint
(linetype=set in the first path plot, and color=set in the second
residual plot). It would be easier for the reader to decode if the set
variable had just one mapping. So in the re-design below we replace
the `geom_point` in the second plot with a `geom_segment` with
`linetype=set`.
Second, we have replaced the single tallrect in the first plot with
two tallrects. The first tallrect has `showSelected=arclength` and is
used to show the selected arclength using a grey rectangle. Since we
specify a `duration` for the `arclength` variable, and the same
`key=1` value, we will observe a smooth transition of the selected
grey tallrect. The second tallrect has `clickSelects=arclength` and so
clicking it has the effect of changing the selected value of
`arclength`. We specify a another data set with more rows, and use the
[named clickSelects/showSelected variables](../Ch06/Ch06-other.html#data-driven-selectors) to
indicate that `arclength` should also be used as a `showSelected`
variable.
```{r Ch11-viz-moving-rect}
tallrect.show.list <- list()
for(a in tallrect.dt$arclength){
is.selected <- tallrect.dt$arclength == a
not.selected <- tallrect.dt[!is.selected]
tallrect.show.list[[paste(a)]] <- data.table::data.table(
not.selected, show.val=a, show.var="arclength")
}
tallrect.show <- do.call(rbind, tallrect.show.list)
animint(
path=ggplot()+
theme_bw()+
theme(panel.margin=grid::unit(0, "lines"))+
facet_grid(y.var ~ ., scales="free")+
ylab("")+
scale_color_manual(values=variable.colors)+
geom_line(aes(
arclength, standardized.coef, color=variable, group=variable),
data=addY(path, "weights"))+
geom_line(aes(
arclength, mse, linetype=set, group=set),
data=addY(mean.error, "error"))+
geom_tallrect(aes(
xmin=arclength-rect.width,
xmax=arclength+rect.width,
key=1),
showSelected="arclength",
alpha=0.5,
data=tallrect.dt)+
geom_tallrect(aes(
xmin=arclength-rect.width,
xmax=arclength+rect.width,
key=paste(arclength, show.val)),
clickSelects="arclength",
showSelected=c("show.var"="show.val"),
alpha=0.5,
data=tallrect.show),
res=ggplot()+
theme_bw()+
geom_hline(aes(
yintercept=residual),
data=hline.dt,
color="grey")+
guides(linetype="none")+
geom_point(aes(
response, residual,
key=observation.i),
showSelected=c("set", "arclength"),
shape=21,
fill=NA,
color="black",
data=lasso.res)+
geom_text(aes(
3, 2.5, label=sprintf("L1 arclength = %.1f", arclength),
key=1),
size=15,
showSelected="arclength",
data=tallrect.dt)+
geom_text(aes(
0, ifelse(set=="subtrain", -2, -2.5),
label=sprintf("%s error = %.3f", set, mse),
key=1),
size=15,
showSelected=c("set", "arclength"),
hjust=0,
data=mean.error[set=="subtrain"])+
geom_segment(aes(
response, residual,
xend=response, yend=0,
linetype=set,
key=observation.i),
showSelected=c("set", "arclength"),
size=1,
data=lasso.res),
duration=list(arclength=2000),
time=list(variable="arclength", ms=2000))
```
## Chapter summary and exercises {#Ch11-exercises}
We created a visualization of the Lasso machine learning model, which
simulataneously shows the regularization path and error
curves. Interactivity was used to show details for different values of
the regularization parameter.
Exercises:
* Re-make this data viz, including the same visual effect for the
tallrects, using only one `geom_tallrect`. Hint: create another data
set with `expand.grid(arclength.click=arclength,
arclength.show=arclength)`, as in the definition of the
`make_tallrect_or_widerect` function.
* Add another scatterplot that shows predicted values versus response,
with a `geom_abline` in the background to indicate perfect
prediction.
* How would the error curves look if other train/validation splits
were chosen? Perform 4-fold cross-validation and add a plot that
can be used to select test fold.
Next, [Chapter 12](../Ch12/Ch12-SVM.html) explains how to visualize the
Support Vector Machine.